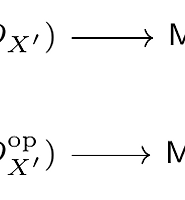아무 블로그
Rational singularity 본문
$\newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\Spec}{\mathrm{Spec}\,} \newcommand{\O}{\mathcal{O}} \newcommand{\bb}[1]{\mathbb{#1}} \newcommand{\d}{\mathrm{d}} \newcommand{\F}{\mathbb{F}} \newcommand{\N}{\mathbb{N}} \newcommand{\P}{\mathbb{P}} \newcommand{\m}{\mathfrak{m}} \newcommand{\GL}{\mathrm{GL}} \newcommand{\et}{\mathsf{\acute{e}t}} \newcommand{\lara}[1]{\langle #1 \rangle} \newcommand{\leris}[1]{\left(#1\right)} \newcommand{\lerim}[1]{\left\{#1\right\}} \newcommand{\leril}[1]{\left[#1\right]} \newcommand{\Hom}{\mathrm{Hom}} \newcommand{\Tor}{\mathrm{Tor}} \newcommand{\Ext}{\mathrm{Ext}} \newcommand{\holim}{\mathrm{holim}} \newcommand{\sep}{\mathrm{sep}} \newcommand{\Gal}{\mathrm{Gal}} \newcommand{\Mod}{\mathsf{Mod}} \newcommand{\coker}{\mathrm{coker}} \newcommand{\Im}{\mathrm{Im}} \newcommand{\Ker}{\mathrm{Ker}} \newcommand{\unr}{\mathrm{unr}} \newcommand{\End}{\mathrm{End}} \newcommand{\op}{\mathrm{op}} \newcommand{\Sh}{\mathsf{Sh}} \newcommand{\Sch}{\mathsf{Sch}} \newcommand{\Set}{\mathrm{Set}} \newcommand{\Alg}{\mathsf{Alg}} \newcommand{\p}{\mathfrak{p}} \newcommand{\colim}{\mathrm{colim}} \newcommand{\Supp}{\mathrm{Supp}} \newcommand{\floor}[1]{\left \lfloor #1 \right \rfloor} \newcommand{\ceil}[1]{\left \lceil #1 \right \rceil}$
찐대수기하에선 다음 종류의 singularity가 유행인 것 같아요.
Definition. $X$가 variety고 어느 resolution of singularities $f:X'\to X$가 있어서 $R^if_*\O_Y=0$ for every $i>0$이고 $f_*\O_{X'}=\O_X$라면 $X$가 rational singularity를 가진다고 말한다. 동치명제로, $\O_X\to Rf_*\O_{X'}$가 quasi-isomorphic이란 게 있다.
제가 언제나 생각하는 것이, 찐대수기하에서의 singularity 분류는 equidimensional한 쪽에 초점이 크게 맞춰져 있단 거예요. rational singularity도 그렇게 다르지 않아요.
rational singularity엔 이런 성질이 있어요.
Lemma. $X$가 projective variety고 $f:X'\to X$가 rational singularity의 그것이고 $\mathcal{E}$가 $X$ 위의 vector bundle일 때
$$ H^i(X,\mathcal{E})\cong H^i(X',f^*\mathcal{E})$$
for all $i$가 된다.
Proof) 먼저 $X$를 통째로 $\P^n$에 넣은 다음에 $X$의 dimension에 대한 induction을 생각하자고요. 이 morphism을 $\imath$라고 하고 $\mathcal{E}$의 일종의 resolution을 생각하자고요.
$$ 0\to \mathcal{E}'\to \bigoplus_i \imath^*\O(n_i)\to \mathcal{E}\to 0$$
이제 $\imath^*\O(n_i)$에 대해서 증명하면 $i$에 대한 induction으로 증명이 끝나고, 먼저 $i^*\O_{\P^n}(1)$에 대해선 아무 $\P^n$의 hyperplane을 $H$라고 하면
$$ 0\to \O_{\P^n}\to \O_{\P^n}(1)\to \O_{\P^n}(1)|_H\to 0$$
이 만들어지고, 이걸 $\imath^*$를 씌우고 맨 처음 생각했던 induction하고 $H^i(X,\mathcal{F})\to H^i(X',f^*\mathcal{F})$란 natural morphism, 여기다가 씌우는 long exact sequence, 그리고 five lemma 생각하면 $n\ge 0$일 때 $H^i(X,\imath^*\O_{\P^n}(n))=H^i(X',f^*\imath^*\O_{\P^n}(n))$이 만들어지지요. $n\le 0$일 때도 비슷하게 해주면 돼요.
Lemma. $X$가 variety고 $f:X'\to X$가 resolution of singularities라고 하가. 그러면 $\O_X\to Rf_*\O_{X'}$가 quasi-isomorphism이란 것과 $X$가 Cohen-Macaulay고 $f_*\omega_{X'}\cong \omega_X$란 것은 동치다.
Proof) $X$가 Cohen-Macaulay고 $f_*\omega_{X'}\cong \omega_X$라고 하자고요. 먼저 Grauert-Riemenschneider vanishng으로 $Rf_*\omega^{\bullet}_{X'}\cong \omega^{\bullet}_X$가 되고, 따라서 Grothendieck duality로
$$ \begin{align}\O_X&\cong R\Hom(\omega^{\bullet}_X,\omega^{\bullet}_X) \\ &\cong R\Hom(Rf_*\omega^{\bullet}_{X'},\omega^{\bullet}_X)\\ &\cong Rf_*R\Hom(\omega^{\bullet}_{X'},\omega^{\bullet}_{X'}) \cong Rf_*\O_{X'}\end{align}$$
로 계산할 수 있지요. 여기서 $f^!\omega^{\bullet}_X=\omega^{\bullet}_{X'}$란 정의를 생각했어요. 다시 Grothendieck duality로
$$ Rf_*\omega^{\bullet}_{X'}\cong R\Hom(Rf_*\O_{X'},\omega^{\bullet}_{X})\cong R\Hom(\O_X,\omega^{\bullet}_X)\cong \omega^{\bullet}_X$$
가 되고, $Y$는 smooth니 $\omega^{\bullet}_{X'}\cong \omega_{X'}[d]$ where $d=\dim X=\dim X'$가 되겠고, 따라서 $h^i(\omega^{\bullet}_X)=R^{i+d}f_*\omega_{X'}=0$ for $i>-d$ by Grauert-Riemenschneider가 되겠고, 따라서 $X$는 Cohen-Macaulay에 $\omega^{\bullet}_X\cong \omega_X[d]$가 되겠지요? 이는 $f_*\omega_{X'}\cong \omega_X$를 만들고요.
Lemma. $X$가 smooth variety면 $X$는 rational singularity를 가진다.
Proof) 자기 자신이 resolution이죠
Lemma. $X$가 rational singularity만 가진다고 하고 $f:X'\to X$가 아무 resolution of singularities일 때 $R^if_*\O_{X'}=0$ for every $i>0$이고 $f_*\O_{X'}\cong \O_X$가 된다.
Proof) 위의 Lemma로 $f_*\omega_{X'}$가 사실은 resolution의 선택에 따라서 독립임을 보이면 되는데, $f':X''\to X$가 또 하나의 resolution이라고 하면 $f'':X'''=X'\times_{X}X''\to X$를 정의할 수 있고 $X'''$가 smooth가 아니면 그냥 이것의 resolution으로 바꿔치기하고, 그러면 $X',X'',X'''$ 모두 smooth니 $g:X'''\to X'$하고 $g':X''\to X$를 생각하면 $g_*\omega_{X'''}=\omega_{X'}$로 (See Corollary B.2.6 in vanishing theorems and singularities in birational geometry...)
$$f'_*\omega_{X''}=f'_*(g'_*\omega_{X'''})=f''_*\omega_{X'''}=f_*(g_*\omega_{X'''})=f_*\omega_{X'}$$
로 둘이 같아지게 되겠지요??
다음이 중요한 모양이에요.
Theorem. (Kovacs) $f:X'\to X$가 morphism between varieties라고 하고 $\alpha:\O_X\to Rf_*\O_{X'}$를 associated natural morphism이라고 하자. $X'$가 rational singularity만 가진다고 하고 $\beta:Rf_*\O_{X'}\to X$가 $\beta\circ \alpha$가 quasi-isomorphism in the derived category일 때 $X$ 역시 rational singularity만 가진다.
Proof) 다음 commutative diagram을 생각할께요.
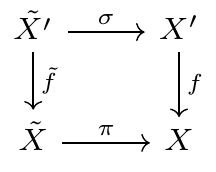
그럼 여기로부터
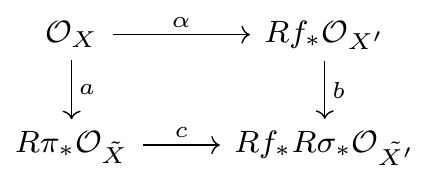
이런 commutative diagram을 얻을 수 있고, $X'$가 rational singularity만 가진단 점에서 $b$는 quasi-isomorphism이 되지요. 따라서
$$ (\beta\circ b^{-1}\circ c)\circ a:\O_X\to R\pi_*\O_{\tilde{X}}\to \O_X$$
는 quasi-isomorphism이 되고 따라서 $X'$를 $\tilde{X'}$로 살짝쿵 바꿔치기하면 $f$가 resolution of singularity라고 가정해도 되지요. 이제
$$ \O_X\overset{\alpha}{\to}Rf_*\O_{X'}\overset{\beta}{\to}\O_X$$
에다가 $R\Hom(-,\omega^{\bullet}_X)$을 씌우면
$$ \omega^{\bullet}_X\overset{\alpha^*}{\gets}Rf_*\omega^{\bullet}_{X'}\overset{\beta^*}{\gets}\omega^{\bullet}_X$$
가 만들어지고 $\alpha^*\circ \beta^*$가 quasi-isomorphism이니
$$ h^i(\omega^{\bullet}_X)\subseteq R^if_*\omega^{\bullet}_{X'}\cong R^{i+d}f_*\omega_{X'}$$
where $d=\dim X=\dim X'$가 되고, Grauert-Riemenschneider로 $h^i(\omega^{\bullet}_X)=0$ for $i>-d$가 만들어지고, 따라서 $X$는 Cohen-Macaulay가 되지요. 이제 $h^{-d}$를 씌우면
$$ \omega_X\overset{h^{-d}(\beta^*)}{\to} f_*\omega_{X'}\overset{h^{-d}(\alpha^*)}{\to}\omega_X$$
가 만들어지고 그 composition은 isomorphism이니 $f_*\omega_{X'}\cong \omega_X$가 돼요. (?? 왜???)
이제 다음을 소개할께요.
Theorem. $X$가 normal complete variety with only rational singularities고 $D$가 $X$ 위의 nef and big Cartier divisor라고 하자. 그러면 모든 $i<\dim X$에 대해서
$$ H^i(X,\O_X(-D))=0$$
이 된다.
Proof) $f:X'\to X$가 rational singularity의 그것이라면 맨 처음 증명했던 lemma로
$$ H^i(X,\O_X(-D))\cong H^i(Y,\O_Y(-f^*D))$$
가 되고, $f$가 birational이란 것으로 $f^*D$는 nef and big이고 따라서 $i<\dim Y=\dim X$에 대해서 Kawamata-Viehweg로 $H^i(X,\O_X(-D))=H^i(Y,\O_Y(-f^*D))=0$이 되지요.
Remark. 바로 위의 theorem에서 $X$가 Cohen-Macaulay니까 $H^i(X,\O_X(K_X+D))=0$ for $i>0$도 쉽게 만들 수 있어요.
'수학 > 기하' 카테고리의 다른 글
| D-module 3 (0) | 2020.08.17 |
|---|---|
| D-module 2 (0) | 2020.08.16 |
| D-module 1 (0) | 2020.08.15 |
| Vanishing theorem 2 (0) | 2020.08.13 |
| Vanishing theorem 1 (0) | 2020.08.12 |