아무 블로그
Abelian variety 3 본문
$\newcommand{\Z}{\mathbb{Z}} \newcommand{\Q}{\mathbb{Q}} \newcommand{\R}{\mathbb{R}} \newcommand{\C}{\mathbb{C}} \newcommand{\Spec}{\mathrm{Spec}\,} \newcommand{\O}{\mathcal{O}} \newcommand{\bb}[1]{\mathbb{#1}} \newcommand{\d}{\mathrm{d}} \newcommand{\F}{\mathbb{F}} \newcommand{\N}{\mathbb{N}} \newcommand{\P}{\mathbb{P}} \newcommand{\m}{\mathfrak{m}} \newcommand{\GL}{\mathrm{GL}} \newcommand{\et}{\mathsf{\acute{e}t}} \newcommand{\lara}[1]{\langle #1 \rangle} \newcommand{\leris}[1]{\left(#1\right)} \newcommand{\lerim}[1]{\left\{#1\right\}} \newcommand{\leril}[1]{\left[#1\right]} \newcommand{\Hom}{\mathrm{Hom}} \newcommand{\Tor}{\mathrm{Tor}} \newcommand{\Ext}{\mathrm{Ext}} \newcommand{\holim}{\mathrm{holim}} \newcommand{\sep}{\mathrm{sep}} \newcommand{\Gal}{\mathrm{Gal}} \newcommand{\Mod}{\mathsf{Mod}} \newcommand{\coker}{\mathrm{coker}} \newcommand{\Im}{\mathrm{Im}} \newcommand{\Ker}{\mathrm{Ker}} \newcommand{\unr}{\mathrm{unr}} \newcommand{\End}{\mathrm{End}} \newcommand{\op}{\mathrm{op}} \newcommand{\Sh}{\mathsf{Sh}} \newcommand{\Sch}{\mathsf{Sch}} \newcommand{\Set}{\mathrm{Set}} \newcommand{\Alg}{\mathsf{Alg}} \newcommand{\p}{\mathfrak{p}} \newcommand{\colim}{\mathrm{colim}}$
abelian variety에 대한 여러가지 (사실 별로 필요 없을 것 같은데 어쩔 수 없이 써야 하는 것 같은) 정리들을 볼 거예요. Milne이 이걸 하는 걸 반쯤 포기한 것 같으니(...) Bhatt의 note를 배낄께요.
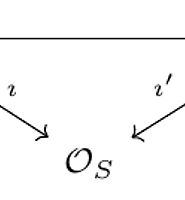
Theorem. $S$가 noetherian scheme이라고 하고 $f:X\to S$가 proper flat map이고 $\mathscr{L}\in \mathrm{Pic}(X)$이 line bundle on $X$라고 하자. 그러면 적당한 locally closed subscheme $Z\subseteq S$이 유일하게 있어서
- $(f_Z)_*(\mathscr{L}_Z)$는 invertible
- $Z$는 다음과 같은 universal property를 만족한다. 그러니까 $T\to S$가 $(f_T)_*(\mathscr{L}_T)$가 invertible이 된단 조건을 만족하면 적당한 factorization $T\overset{g}{\to}Z\hookrightarrow S$가 있어서 $(f_T)_*(\mathscr{L}_T)\to g^*((f_Z)_*(\mathscr{L}_Z))$는 isomorphism이 된다.
그냥 적당한 closed subscheme이 있어서 거기에선 pushforward도 line bundle이란 내용이네요.
Proof) 저런 $Z$가 있다면 universal property는
$$ Z=\{s\in S|H^0(X_s,L_s)\text{ is 1-dimensional}\}$$
가 돼요. 그럼 semicontinuity theorem(cf. Hartshorne 3.12, Theorem. 8)로 $Z$는 locally closed가 되겠지요?? 이제 먼저 $Z$의 underlying topological space를 그냥 저렇게 줄께요.
그럼 이 set을 그냥 정의한 다음에 여기에 scheme structure를 주면 모든 게 끝인데, 이는 $S$가 affine scheme이라고 가정해도 되겠지요
그럼 finite $A$-module $B$에 대해서 $\mathscr{L}$의 cohomology를 계산하는 perfect complex $M^{\bullet}$을 하나 잡으면($f$가 proper flat이라 있다고 하네요. 그냥 Cech cover로 잡으면 각각이 finite $A$-module이란 건 proper에서 오고 그럼 noetherian condition으로 각각의 term의 projective resolution을 잡을 수 있고 total complex를 생각하면 우리가 잡은 게 perfect complex임을 알 수 있고 이것은 tensoring되어도 $f$에 붙은 flatness condition으로 여전히 perfect complex가 되지요!!)
$$ H^0(X_B,\mathscr{L}_B)\cong H^0(M^{\bullet}\otimes_A B)\cong \Hom_A(Q,B)$$
가 될 거예요. 여기서
$$ Q=\mathrm{coker}\,\left((M^1)^{\vee}\to (M^0)^{\vee}\right)$$
고요. 그럼 $H^0(X_s,\mathscr{L}_s)$가 $1$-dimensional이란 것은 저 계산에서 $B$를 $s$를 중심으로 줄여간다면 $Q\otimes \kappa(s)$가 $1$-dimensional이란 걸 뜻하고 Nakayama lemma는 $Q$가 rank $1$이란 걸, 그러니까 적당한 ideal $I$가 있어서 $A$-module로 $Q\cong A/I$란 사실을 알려주게 되지요. 그러면 우리가 원하는 건 $|Z|=V(I)$고, 그냥 $V(I)$가 저 universal property를 만족함을 보이면 되겠고 첫번째는 자명하고 두번째는 $1\in A$가 $B$의 어느 원소로 대응되는데 여기에 $I$의 원소를 곱하면 $0$이 되어야 하니까
$$ \Hom_A(Q,B)\cong \{b\in B|bI=0\}$$
으로 계산될 수 있고 따라서 $IB=0$이면 저 계산결과로 $bI=0$ for all $b\in B$로 $\Hom_A(Q,B)\cong B$ as $B$-module이고 $\Hom_A(Q,B)\cong B$이면 $f\in \Hom_A(Q,B)$일 때 $f(1)$에 $I$의 어떤 원소를 곱해도 $0$이 되어야 하니까 $IB=0$이겠지요??
이제 다음을 증명할께요
Theorem. (Seesaw principle)
$f:X\to S$가 proper flat morphism이라고 하고 fibre들이 geometrically integral이라고 하자. $\mathscr{L}\in \mathrm{Pic}(X)$가 $X$의 line bundle이라고 하면
- $Z:=\{s\in S|\mathscr{L}_s\text{ is trivial }\}$는 $S$에서 closed가 된다.
- $\mathscr{L}_{Z_{\mathrm{red}}}$는 pullback from $Z_{\mathrm{red}}$가 된다.
- $Z$엔 unique closed subscheme structure가 있어서 $\mathscr{L}_Z$는 $Z$의 pullback이 되고 $Z$는 이런 성질에 대해서 universal하다.
정말로 직관적으로 생각한다면, 위에서 $X=Y\times S$라고 생각하고 $Z$를 $\mathscr{L}_{X\times \{t\}}$가 trivial한 $t$들을 모았다고 생각해봐요. 아예 대수기하를 벗어나서(...) 그냥 $Y=S^1$이라고 생각하고 $T$는 line이라고 생각한다면, $T$의 모든 점에서 line bundle이 trivial하다고 하면 그 trivial하게 만드는 isomorphism이 있을 거예요. 이를 $\alpha_t$정도로 쓴다면 이는 언제나 $>0$이거나 $<0$이거나 해야 해요!! 둘 중 하나가 아니라면 결국 $0$이 되는 점이 생기고, 이 땐 isomorphism이 아니게 되겠지요. 이는 모순이에요. 그리고 이렇게 되면 적당히 gluing을 잘 조절해서 $\alpha_t=1$이나 $\alpha_t=-1$이 되도록 할 수 있지요. 이는 $X$가 proper scheme이어야 하는데 저 trivial이 되는 곳들을 closed subscheme으로 만들기 위한 technical condition이에요. 그리고 이거 저 아직도 "시소"란 이름이 붙은 이유를 모르겠어요 (...)
Proof) 첫번째는 geometrically integral scheme에서 line bundle이 trivial하기 위한 필충은 자기 자신과 그 inverse가 모두 nonzero section을 가지는 거예요. (증명 쉬워요) 따라서
$$ Z=\{s\in S|H^0(X_s,\mathscr{L}_s)\ne 0\}\cap \{s\in S|H^0(X_s,\mathscr{L}^{-1}_s)\ne 0\}$$
가 되고, 따라서 semicontinuity theorem을 또 쓰면 이것도 closed가 되겠지요??
두번째는 귀찮으니(...) $S=Z_{\mathrm{red}}$라고 하자고요. 그리고 $\mathscr{M}=f_*\mathscr{L}$라고 할께요. 그럼 $M$이 $S$ 위의 line bundle이란 건 local하게 생각하면 Nakayama로 쉽게 알 수 있고, 남은 건 $f^*\mathscr{M}\to L$이란 unit map이 isomorphism이란 건데, 이것도 똑같이 fibrewise하게 생각한 다음에 Nakayama를 생각하면 돼요.
세번째는 $S$-scheme $T$가 있을 때 $(f_T)_* \mathscr{L}_T$하고 $(f_T)_*\mathscr{L}^{\vee}_T$가 동시에 invertible할 때 $\mathscr{L}_T$가 $T$로부터 pulled back됨을 증명하는 것은 쉬워요. 그리고 위에서 증명한 것으로 이런 것이 만족되는 maximal loclaly closed subscheme $W\subseteq S$가 있고, 그냥 $W=Z$네요
Milne에서의 증명도 비슷비슷한 것 같아요.
이제 다음을 볼께요!!
Theorem. $S$가 connected noetherian scheme이라고 하자. 그리고 $X\to S$하고 $Y\to S$가 proper flat morphism이라고 하고 둘 다 geometrically integral fibre를 가진다 하자 $\mathscr{L}\in \mathrm{Pic}(X\times_S Y)$라고 하고
- $e_X\in X(S), e_Y\in Y(S)$가 있어서 $\mathscr{L}|_{\{e_X\}\times_S Y}$하고 $\mathscr{L}|_{X\times_S \{e_Y\}}$는 trivial
- $s\in S$가 있어서 $L|_{X_s\times_s Y_s}$는 trivial
그러면 $\mathscr{L}$은 $S$로부터 pulled back된다.
Proof) $\pi:P:=X\times_S Y\to S$를 정의하고 (첫번째 조건을 써서) $Z\subseteq S$가 $\mathscr{L}_{P_Z}$가 $Z$로부터 나오는 가장 큰 closed subscheme이라고 할께요. 이는 시소 정리로부터 나와요. 그럼 당연히 증명해야 할 건 $Z=S$일 거예요.
이제 $Z$가 closed under generalization임을 증명하기만 하면 되고, 따라서 $S=\Spec R$에서 $R$이 noetherian local ring이라고 해도 되고, $I$가 $Z$의 ideal sheaf의 global section이라고 하고 $R$가 discrete valuation ring이라고 해도 induction과 localization으로 될 거예요. 그럼 $I=0$임을 증명하면 되겠네요. $\m$을 $R$의 maximal ideal이라고 할께요.
$I\ne 0$이면 어떤 $J\subseteq I$가 있어서 $I/J\cong k=R/\m$이 되고, $W=\Spec R/J$라고 하면 $Z\subsetneq W\subseteq S$고 그러면 $W$는 저 pullded back의 관점에서 maximal이 될 수 없어요.
line bundle over local ring은 당연히 죄다 trivial하니 $\mathscr{L}_{P_Z}$도 $Z$의 정의로 trivial하겠고 이제 $\mathscr{L}_{P_W}$가 trivial함을 확인한다면 $Z$의 정의에 모순이 되겠지요?? 당연히 이걸 증명하는 건 exact sequence와 cohomology질(...)인데,
$$ 0\to k\to R/J\to R/I\to 0$$
에서
$$ 0\to \mathscr{L}_{P_s}\to \mathscr{L}_{P_W}\to \mathscr{L}_{P_Z}\to 0$$
이란 게 만들어지고 이는 flatness of $\pi$에서 정말로 exact예요. 이제 trivialness를 생각해서 $\alpha$라는 $\mathscr{L}_{P_Z}$의 trivialization을 선택하고, $\alpha$가 $H^0(P_W,\mathscr{L}_{P_W})$로 lift된다면 $\mathscr{L}_{P_W}$도 trivial이 되면서 모든 것이 끝나요. 이는 저 exact sequence를 봤을 때
$$ H^0(P_Z,\mathscr{L}_{P_Z})\to H^0(P_W,\mathscr{L}_{P_W})\to H^1(P_s,\mathscr{L}_{P_s})$$
라는 long exact sequence를 생각하고 여기에서 boundary map을 $\delta$라 한다면 $\delta(\alpha)=0$이면 되는 일이고요. 그리고 $\delta(\alpha)$는
$$ H^1(P_s,\mathscr{L}_{P_s})\to H^1(X_s,\mathscr{L}_s)\times H^1(Y_s,\mathscr{L}_s)$$
라는 map에 의해서 (두번째 조건으로) $0$으로 보내지고, Kunneth formula로 그냥 $\delta(s)=0$이네요.
이제 다음을 증명할께요!!
Theorem. (Theorem of the cube) $X\to S, Y\to S$가 proper flat morphisms with geometrically integral fibres라고 하자. 그리고 $Z$가 connected $S$-scheme of finite type이라고 하자. 그러면 $\mathscr{L}\in \mathrm{Pic}(X\times_S Y\times_S Z)$가 line bundle이고 $x\in X(S), y\in Y(S), z\in Z(S)$가 있어서 $\mathscr{L}|_{X\times Y\times \{z\}}, \mathscr{L}|_{X\times \{y\}\times Z}, \mathscr{L}|_{\{x\}\times Y\times Z}$가 모두 trivial이면 $\mathscr{L}$도 trivial이다
Proof) 위의 theorem을 $X\times_S Y, Y\times_S Z$에 대해서 적용해볼께요. 그리고
$$ X\times_S Y\times_S Z=(X\times_S Z)\times_Z (Y\times_S Z)\to Z$$
를 생각하면 위의 모든 조건이 맞아 떨어진다는 걸 알 수 있어요 신기하다!!
다음을 증명할께요.
Lemma. $A$가 abelian variety over $k$라고 하고 $Z$가 $k$-scheme이라고 하고 $f,g,h:Z\to A$가 있다고 해보자. 그러면 line bundle $\mathscr{L}\in \mathrm{Pic}(A)$에 대해서
$$ (f+g+h)^*\mathscr{L}\cong (f+g)^*\mathscr{L}\otimes (g+h)^*\mathscr{L}\otimes (f+h)^*\mathscr{L}\otimes f^*\mathscr{L}^{-1}\otimes g^*\mathscr{L}^{-1}\otimes h^*\mathscr{L}^{-1}$$
이 된다.
Proof) (Sketch) $Z=A\times A\times A$라고 둬도 되겠고 $m_{fgh}=f+g+h$등등으로 두면 위의 theorem을 쓰기 위해서 $0\in A(k)$를 생각하면 조건이 모두 맞아 떨어지면서 증명이 끝나요.
Corollary. $A/k$가 abelian variety라고 하고 $[n]:A\to A$를 $a$를 이것을 $n$번 더하는 것으로 보내는 morphism이라고 하자. 그러면
$$ [n]^*\mathscr{L}=\mathscr{L}^{\frac{n^2+n}{2}}\otimes (-1)^*\mathscr{L}^{\frac{n^2-n}{2}}$$
가 된다
Proof) (Sketch) induction을 써요. $n=1$일 때는 당연하고 $n=n_0$ 이하일 때 일 때 성립하면 $n=n_0+1$일 땐 $f=[n], g=[1], h=[-1]$이라고 하고 위 lemma를 쓰면
$$ [n+1]^*\mathscr{L}\cong [n]\mathscr{L}\otimes [n-1]^*\mathscr{L}^{-1}\otimes \mathscr{L}\otimes [-1]^*\mathscr{L}$$
이 나오고 induction hypothesis를 쓰면 될 거예요.
Corollary. (Theorem of the square)
$t_a:A\to A$를 $a$를 더하기라고 생각하면
$$t^*_{a+b}\mathscr{L}\otimes t^*_a\mathscr{L}^{-1}\otimes t^*_b\mathscr{L}^{-1}\otimes \mathscr{L}$$
은 trivial이다.
Proof) 이번엔 저 lemma에 $f=1, g=t_a, h=t_b$를 대입하자고요.
다음엔 isogenies에 대해서 해볼께요.
'수학 > 정수론' 카테고리의 다른 글
| Abelian variety 5 (0) | 2020.04.29 |
|---|---|
| Abelian variety 4 (0) | 2020.04.29 |
| Abelian variety 2 (0) | 2020.04.29 |
| Abelian variety 1 (0) | 2020.04.29 |
| Selmer complex 1 (0) | 2020.03.08 |